Answer:
60 liters fruit juice.
40 liters ginger ale.
Explanation:
Let g represent ginger ale and f represent fruit juice.
We have been given that Sharon is making 100 liters of punch for a party. The punch contains ginger ale (g) and fruit juice (f). We can represent this information in an equation as:

The cost of ginger ale is $1 per liter and the fruit juice is $1.50 per liter. Sharon spent a total of $130.
We can represent this information in an equation as:
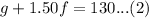
Now, we will use substitution method to solve system of equations. From equation (1) we will get,
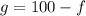
Substituting this value in equation (2) we will get,

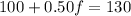
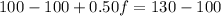
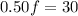
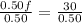

Therefore, Sharon put 60 liters of fruit juice in the punch.
Now, we will substitute
 in equation (1).
in equation (1).


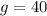
Therefore, Sharon put 40 liters of ginger ale in the punch.