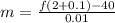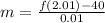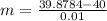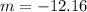Answer:
(i)
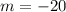
(ii)

(iii)

(iv)
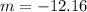
Explanation:
The given function is
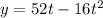
where, h is the height of ball after t seconds.
It can be written as
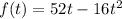
At x=2,
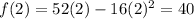
The average of a function f(x) on [a,b] is
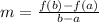
The time period beginning when t = 2 and lasting with h.
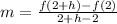
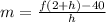
(i)
Here, h = 0.5 second

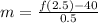
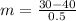
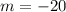
(ii)
Here, h = 0.1 second
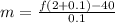
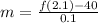


(iii)
Here, h = 0.05 second

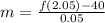
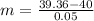

(iv)
Here, h = 0.01 second