Question

What is the area of the triangle whose vertices are X(−5, −1)) , Y(−5, −10)) , and Z(−9, −7) ?

____Units sqared

Answer 1

XY = −1−(−10) = 9
(line x = −5) = −5−(−9) = 4

Area = 1/2 * 9 * 4 = 18

Answer 2

17.96 units squared

Explanation:

Refer the attached figure .

Point X = (−5, −1)

Point Y=(−5, −10)

Point Z=(−9, −7)

In ΔXYZ , to find the length of sides we will use distance formula.

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

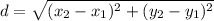
Length of XY

Point X =
`(x_1,y_1)=(-5,-1)`

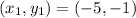
Point Y=
`(x_2,y_2)=(-5,-10)`

`XY=√((-5-(-5))^2+(-10-(-1))^2)`

`XY=√((0)^2+(-9)^2)`

`XY=√(81)`

`XY=9`

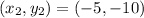
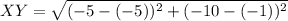
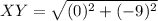
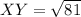
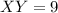
Length of YZ

Point Y=
`(x_1,y_1)=(-5,-10)`

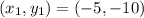
Point Z =
`(x_2,y_2)=(-9,-7)`

`YZ=√((-9-(-5))^2+(-7-(-10))^2)`

`XY=√((-4)^2+(3)^2)`

`YZ=√((-4)^2+(3)^2)`

`YZ=√(16+9)`

`YZ=√(25)`

`YZ=5`

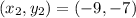
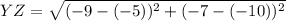
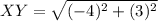
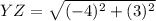
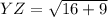
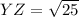
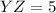
Length of XZ

Point X =
`(x_1,y_1)=(-5,-1)`

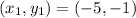
Point Z =
`(x_2,y_2)=(-9,-7)`

`XZ=√((-9-(-5))^2+(-7-(-1))^2)`

`XZ=√((-4)^2+(-6)^2)`

`XZ=√(16+36)`

`XZ=√(52)`

`XZ=7.2`

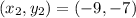
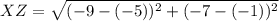
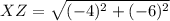
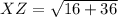
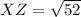
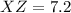
So, to find the area of triangle we will use heron's formula .

`Area =√(s(s-a)(s-b)(s-c))`

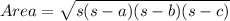
Where
`s=(a+b+c)/(2)`

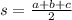
a,b,c are sides of triangle

a=9

b=5

c=7.2

`s=(9+5+7.2)/(2)`

`s=10.6`

`Area =√(10.6(10.6-9-a)(10.6-5)(10.6-7.2))`

`Area =√(322.9184)`

`Area =17.96`

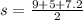
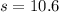
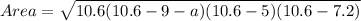
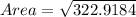
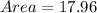
Hence the area of triangle is 17.96 units squared