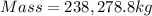Question

A cylindrical tank with a radius of 10 ft and a height of 40 ft is filled with gasoline. given a density of 670 kg/m 3 , determine the mass (lbm) of the gasoline in the tank.

Answer 1

`Mass=238,278.8 kg`

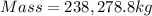
Explanation:

Given: radius of cylindrical tank = 10 ft=10×0.3048=3.048m and height of the cylindrical tank=40ft=40×0.3048=12.192m.

Volume of cylindrical tank=
`{\pi}r^(2)h`

=
`3.14(3.048)^2(12.192)`

=
`3.14(9.290)(12.192)`

=
`355.64m^3`

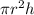
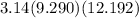
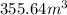
Therefore, the volume of the cylindrical tank=
`355.64m^3`

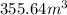
Now, We know that Density=
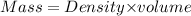
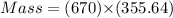
`(Mass)/(Volume)`

⇒
`Mass=Density{*}volume`

⇒
`Mass=(670){*}(355.64)`

⇒
`Mass=238,278.8 kg`

Answer 2

Cylinder:
V = r² π h
r = 10 ft = 10 * 0.3048 m = 3.048 m , h = 40 ft = 40 * 0.3084 = 12.336 m.
Density: m / V = 670 kg/m³
V = 3.048 ² · 3.14 · 12.336 = 359.86 m³
m = V · D = 359.86 m² · 670 kg/m³
Answer:
m = 241,106.4 kg.