Question

Log(x) + log(x + 3) = 7

Answer 1

`x=3160.778016...`

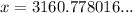
Explanation:

Given logarithmic equation:

`\log(x)+\log(x+3)=7`

`\textsf{Apply the product log law}: \quad \log_axy=\log_ax + \log_ay`

`\implies \log(x(x+3))=7`

`\implies \log(x^2+3x)=7`

`\textsf{Apply the log law}: \quad \log_ab=c \iff a^c=b`

`\implies x^2+3x=10^7`

`\implies x^2+3x-10000000=0`

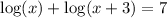
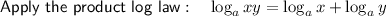
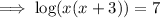
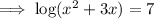
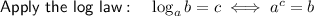
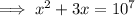
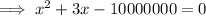
Solve the quadratic equation by using the quadratic formula.

Quadratic Formula

`x=(-b \pm √(b^2-4ac))/(2a)\quad\textsf{when }\:ax^2+bx+c=0`

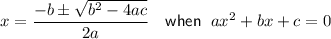
Therefore:

`a=1, \quad b=3,\quad c=-10000000`

Substitute the values of a, b and c into the quadratic formula:

`\implies x=(-3 \pm √(3^2-4(1)(-10000000)))/(2(1))`

`\implies x=(-3 \pm √(9+40000000))/(2)`

`\implies x=(-3 \pm √(40000009))/(2)`

`\implies x=3160.778016..., \quad x=-3163.778016...`

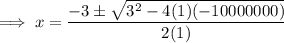
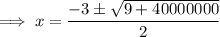
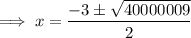
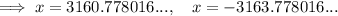
As logs of negative numbers cannot be taken, the only valid solution is:

`\boxed{x=3160.778016...}`