Final answer:
The general term of the given sequence is 10 to the power of 3 times the term number (
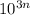 ) starting from n=0. This sequence showcases the use of powers of ten, which is fundamental in expressing numbers in scientific notation.
) starting from n=0. This sequence showcases the use of powers of ten, which is fundamental in expressing numbers in scientific notation.
Step-by-step explanation:
The given sequence is 1, 1,000, 10,000,000, 1,000,000,000,000,000,... This sequence can be described using powers of ten. On close observation, we can notice that the exponents of 10 increase in a particular pattern. The first term has 10 to the power of 0 (10^0), which is 1, the second term is 10^3 which equals 1,000, the third term is 10^6 for 10,000,000, and so on. The pattern is that the exponent increases by 3 with each term. Hence, the general term of the sequence can be expressed as
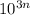 , where n is the term number starting from 0, 1, 2, ...
, where n is the term number starting from 0, 1, 2, ...
To verify, we can substitute the term numbers:
- n=0: 10^3(0) = 100 = 1
- n=1: 10^3(1) = 103 = 1,000
- n=2: 10^3(2) = 106 = 10,000,000
This confirms our formula for the general term.