Question

A 110 kg tackler moving at 2.5m/s meets head on (and holds on to) an 82 kg halfback moving at 5.0m/s. what will be their mutual speed immediately after the collision?!

Answer 1

0.7 m/s

Step-by-step explanation:

We can solve the problem by using conservation of momentum.

Before the collision, the momentum of the first tackler is:

`p_1 = m_1   v_1 =(110 kg)(2.5 m/s)=275 kg m/s`

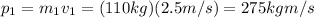
while the momentum of the second tackler is

`p_2 = m_2 v_2 =(82 kg)(-5.0 m/s)=-410 kg m/s`

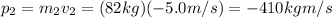
Note that we used a negative sign because the direction of the second tackler is opposite to that of the first tackler.

Therefore, the total momentum before the collision is

`p_i = p_1 +p_2 =275 kg m/s -410 kg m/s=-135 kg m/s`

Since the total momentum is conserved, this is also equal to the final total momentum :

`p_f = -135 kg m/s`

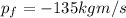
Which is also equal to

`p_f = (m_1 +m_2 )v_f`

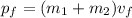
since the two tacklers continue their motion together with final velocity vf. Re-arranging the previous equation, we can find the the new velocity of the two tacklers:

`v_f = (p_f)/(m_1 +m_2)=(-135 kg m/s)/(110 kg + 82 kg)=-0.7 m/s`

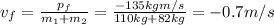
and the negative sign means the direction is the one of the second tackler.