Question

What are the coordinates of the turning point for the function f(x) = (x+3)^3 + 1

Answer 1

The turning point is just the minimum/maximum so the coordinates are (-3,1) which you find from the expression of (x+3)³ + 1

Answer 2

The turning points for the given function is (-3,1).

Explanation:

The given function is

`f(x)=(x+3)^3+1`

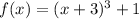
The turning point of a function where the
`f'(x)=0`.

`f'(x)=3(x+3)^2`

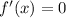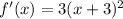
Equate the first derivative equals to 0.

`0=3(x+3)^2`

`x+3=0`

`x=-3`

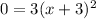
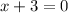
At the turning point the x-coordinate is -3.

Substitute x=-3 in the given function.

`f(-3)=(-3+3)^3+1`

`f(-3)=1`

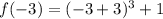
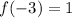
At the turning point the y-coordinate is 1.

Therefore the turning point is (-3,1).