Answer: The correct statements are
The GCF of the coefficients is correct.
The variable c is not common to all terms, so a power of c should not have been factored out.
David applied the distributive property.
Explanation:
GCF = Greatest common factor
1) GCF of coefficients : (80,32,48)
80 = 2 × 2 × 2 × 2 × 5
32 = 2 × 2 × 2 × 2 × 2
48 = 2 × 2 × 2 × 2 × 3
GCF of coefficients : (80,32,48) is 16.
2) GCF of variables :(
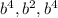 )
)
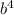 = b × b × b × b
= b × b × b × b
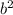 = b × b
= b × b
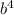 =b × b × b × b
=b × b × b × b
GCF of variables :(
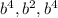 ) is
) is
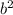
3) GCF of
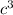 and c: c is not the GCF of the polynomial. The variable c is not common to all terms, so a power of c should not have been factored out.
and c: c is not the GCF of the polynomial. The variable c is not common to all terms, so a power of c should not have been factored out.
4)
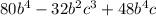
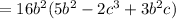
David applied the distributive property.