Question

In the function f(t)= 200(.95)^t what is the rate of change

Answer 1

F(t) = 200(0.95)^t = 200(1 - 0.05)^t
rate is 5% decay per unit of time.

Hopefully that is correct & I hope I helped :)

Answer 2

The rate of change is 5%.

Explanation:

Given : Function
`f(t)=200(0.95)^t`

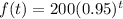
To find: What is the rate of change?

Solution :

The given function is an exponential function as it is in form
`f(x)=ab^x`

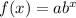
in which b is the factor of rate,

If b=1+r then r is the growth rate

If b=1-r then r is the decay rate.

We have given b=0.95

So, 0.95=1-r

r=1-0.95

r=0.05

i.e, It is a decay rate with 5%.

Therefore, The rate of change is 5%.