Question

Using the given zero to find the remaining zeros of the function f(x)=x^3-4^2+49x-196; zero: -7i

Answer 1

Because
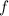
`f` has real coefficients, you know the complex root occurs along with its conjugate. That is, both
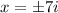
`x=\pm7i` are roots to
`f(x)`.

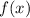
This means that dividing through by both factors yields another polynomial with no remainder:


`(x^3-4x^2+49x-196)/((x-7i)(x+7i))=(x^3-4x^2+49x-196)/(x^2+49)=x-4`

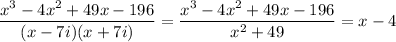
This means the last root (there are only three according to the fundamental theorem of algebra) is
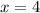
`x=4`.