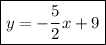Answer:

Explanation:
A perpendicular bisector is a line that intersects another line segment perpendicularly and divides it into two equal parts.
Given endpoints of the line segment:
- (x₁, y₁) = (-3, 2)
- (x₂, y₂) = (7, 6)
Substitute the given endpoints into the slope formula to find the slope of the line segment:
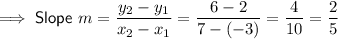
If two lines are perpendicular to each other, their slopes are negative reciprocals.
Therefore, the slope of the perpendicular line is -⁵/₂.
Find the midpoint of the given line segment by substituting the given endpoints into the midpoint formula:
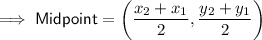
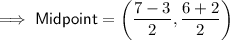
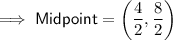
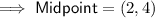
To find the equation of the perpendicular bisector, substitute the found slope and midpoint into the point-slope form of a linear equation:

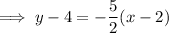
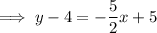
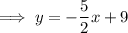
Therefore, the equation for the perpendicular bisector of the line segment whose endpoints are (-3, 2) and (7, 6) is: