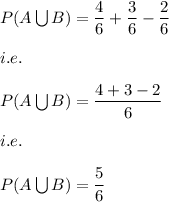Question

A standard number cube is tossed. find p(greater than 2 or even).

Answer 1

=4/6
=2/3

There are 4 numbers greater than 2, which also contains the two even numbers (4 and 6) so the set = {3, 4, 5, 6} which is four numbers of a total 6 so therefore the p = 4/6 which =2/3

Answer 2

Hence, we get:

`P(\text{Greater\ than\ two\ or\ even})=(5)/(6)`

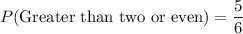
Explanation:

Let A denote the event that the number is greater than 2.

and B denote the event that the number is even.

Let P denote the probability of an event.

Then we are asked to find:

P(A∪B)

We know that:

P(A∪B)=P(A)+P(B)-P(A∩B)

Now, we know that:

`P(A)=(4)/(6)`

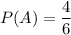
( Since, there are a total of 4 numbers which are greater than 2 i.e. {3,4,5,6} )

Also,

`P(B)=(3)/(6)`

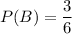
( Since there are a total of 3 numbers which are even.

i.e. {2,4,6} )

Also,

`P(A\bigcap B)=(2)/(6)`

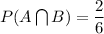
( Since there are two elements which are both even as well as greater than 2 i.e. {4,6} )

Hence, we have:

`P(A\bigcup B)=(4)/(6)+(3)/(6)-(2)/(6)\\\\i.e.\\\\P(A\bigcup B)=(4+3-2)/(6)\\\\i.e.\\\\P(A\bigcup B)=(5)/(6)`