Question

A can manufacturing company is designing a can of cat food to hold 5.5 oz or about 163 cm(3). They have written out that the equation for the surface area for a can with the volume is S=2pie radius(2) + 163/r. Explain why the equation is wrong and how to fix it.

Answer 1

The correct equation that describes the surface area is
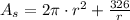`A_(s) = 2\pi \cdot r^(2)+(326)/(r)` and we need to multiply
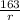`(163)/(r)` by 2 in the equation described in the statement to correct the equation.

Explanation:

Let suppose that the can of cat food is a right cylinder. The surface area of the cylinder (
`A_(s)`), measured in square centimeters, is the sum of the areas of the circular walls (
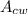`A_(cw)`) and the non-circular wall (
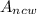`A_(ncw)`), both measured in square centimeters. That is:

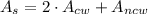`A_(s) = 2\cdot A_(cw)+A_(ncw)` (1)

By Geometry, we expanded the equation above:

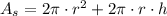`A_(s) = 2\pi\cdot r^(2)+2\pi\cdot r\cdot h` (1b)

Where:

`r` - Radius, measured in centimeters.

`h` - Height, measured in centimeters.

And the volume of the right cylinder (
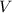`V`), measured in cubic cnetimeters, is defined by the following formula:

`V = \pi\cdot r^(2)\cdot h`

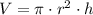
Then, we clear the height of the cylinder within the volume formula:

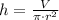`h = (V)/(\pi\cdot r^(2))` (2)

By substituting in (1b), we obtain the following equation:

`A_(s) = 2\pi \cdot r^(2) + 2\pi\cdot r\cdot \left((V)/(\pi\cdot r^(2)) \right)`

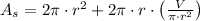
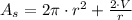`A_(s) = 2\pi\cdot r^(2)+(2\cdot V)/(r)` (1c)

If we know that
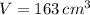`V = 163\,cm^(3)`, then the equation for the surface area of the cylinder is:

`A_(s) = 2\pi \cdot r^(2)+(326)/(r)`

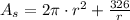
In a nutshell, we need to multiply
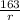`(163)/(r)` by 2 to correct the equation.