Question

a circle has a center (3,5) and a diameter AB. The coordinates of A are (-4,6). what are the coordinates of B?

Answer 1

Find the length of the radius.


`r= √((3-(-4))^2+(5-6)^2) \\r = √(7^2+(-1)^2) \\r= √(50) \\ r=5 √(2)`

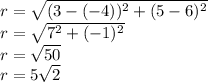
Find the length of the diameter.

d = 2r = 2 × 5√2 = 10√2

Point B must lie on a line AC, where C is a center of a circle.
Find equation of line AC.
A(–4, 6), C(3, 5)


`y-y_1= (y_2-y_1)/(x_2-x_1)(x-x_1) \\y-6= (5-6)/(3-(-4)) (x-(-4)) \\y-6=- (1)/(7) (x+4) \\7y-42=-x-4 \\x+7y-38=0`

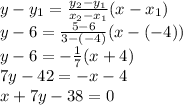
The distance from B(x, y) to C(3, 5) is 5√2.

`√((x-3)^2+(y-5)^2)=5 √(2) \\(x-3)^2+(y-5)^2=(5 √(2))^2 \\(x-3)^2+(y-5)^2=50`

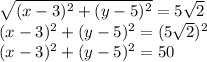
Solve system of equations.

`x+7y-38=0 \\(x-3)^2+(y-5)^2=50 \\ \\x=38-7y \\(38-7y-3)^2+(y-5)^2=50 \\(35-7y)^2+(y-5)^2=50 \\1225-490y+49y^2+y^2-10y+25-50=0 \\50y^2-500y+1200=0 \\y^2-10y+24=0 \\y^2-6y-4y+24=0 \\y(y-6)-4(y-6)=0 \\(y-6)(y-4)=0 \\y_1=6,y_2=4`


`x_1=38-7y_1=38-7 * 6 = 38-42=-4 \\x_2=38-7y_2=38-7 * 4 = 38-28=10`

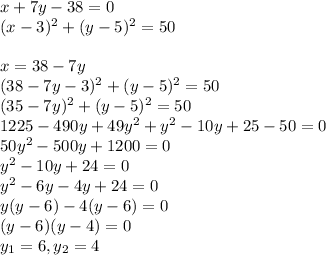
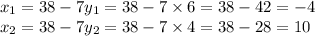
Point B could have coordinates

`\\ \\(x_1,y_1)=(-4,6),(x_2,y_2)=(10,4)`

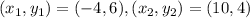
But (–4, 6) are the coordinates of point A.
Therefore, point B has coordinates (10,4).