Question

Find the measure of ∠C if

∠A = 3 2 x + 20
∠B = 7 2 x + 20
∠C = 5 2 x + 40
∠D = 3 2 x + 10

Answer 1

`(32x+20) + (72x+20) + (52x+40) + (32x+10)=180 \\ 32x+72x+52x+32x +20+20+40+10 =180 \\ 188x+90=180 \\ -90 \\ 188x=90 \\ /188 \\ x=0.478`
then
`52(0.478)+40 \\ 24.856+40=64.856`
∠C = 64.856

Answer 2

The measure of angle C is 114.672°

Explanation:

Given: Measure of angles as

∠A = 32x + 20

∠B = 72x + 20

∠C = 52x + 40

∠D = 32x + 10

we have to find the measure of angle C.

Consider the given angles.

Since, there are four angles, so the figure must be a quadrilateral.

Also, we know,

Sum of measure of angles of a quadrilateral is 360°

Thus, ∠A + ∠B + ∠C + ∠D = 360°

Substitute the values , we get,

32x + 20 + 72x + 20 + 52x + 40 + 32x + 10 =360

188x + 90 = 360

188x = 270

`x=(270)/(188)=1.436`

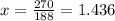
Thus, Measure of angle C is 52(1.436) + 40 =114.672

Thus, The measure of angle C is 114.672°