Question

The half–life of rubidium–89 is 15 minutes. If the initial mass of the isotope is 250 grams, how many grams will be left after 100 minutes?

Answer 1

A: 2.46 grams

Explanation:

Got it correct :)

Answer 2

32.5 grams will be left after 100 minutes.

Explanation:

Given : The half–life of rubidium–89 is 15 minutes. If the initial mass of the isotope is 250 grams.

To find : How many grams will be left after 100 minutes?

Solution :

Let the exponential equation of rubidium is
`Q=Q_oe^(rt)`

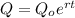
Where,
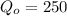`Q_o=250` is the initial value

t is the time taken i.e. t=15 minutes

The half–life of rubidium–89 is 15 minutes.

i.e.
`Q=(Q_o)/(2)`

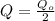
Substitute in the formula,

`(Q_o)/(2)=Q_oe^(r* 15)`

`(1)/(2)=e^(r* 15)`

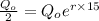
Taking log both side,

`\log ((1)/(2))=r* 15`

`-0.301=r* 15`

`(-0.301)/(15)=r`

`r=-0.02`

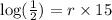
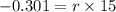
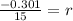
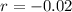
Now, we have to find Q in 100 minutes,

`Q=Q_oe^(rt)`

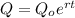
Substitute in the formula,

`Q=250e^(-0.02* 100)`

`Q=250e^(-2)`

`Q=250* 0.13`

`Q=32.5`

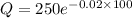
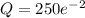
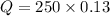
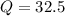
Therefore, 32.5 grams will be left after 100 minutes.