Question

Write in form a√b √20×√2

Answer 1

I would first suggest you to find the square root of 20. This means that you need to find two factors, one of which needs to be a perfect square. Seems like 4 x 5 can work because 4 is a perfect square.

So
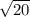
`√(20)` can also be written as
`√(4) * √(5)`. We know that the square root of 4 is 2. Thus, the square root of 20 is 2 times the square root of 5 (
`2 √(5)`).

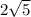
We now have
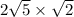
`2 √(5) * √(2)` and since 2 is not a perfect square we cannot really simplify it any further. Therefore, we just multiply the square root of 5 and the square root of 2 because they are under the radical sign. So we get
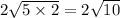
`2 √(5 * 2) = 2√(10)`.

Answer 2

sqrt20 * sqrt2 = sqrt 40 = sqrt4 * sqrt10  = 2 sqrt10