Question

NO LINKS!! Describe the domain and range (in BOTH interval and inequality notation) for each function shown. ​

Answer 1

Answers:

Domain as an inequality:
`\boldsymbol{-\infty < \text{x} < \infty}`

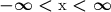
Domain in interval notation:
`\boldsymbol{(-\infty , \infty)}`

Range as an inequality:
`\boldsymbol{-3 \le \text{y} \le 3}`

Range in interval notation: [-3, 3]

=================================================

Step-by-step explanation:

The domain is the set of allowed x inputs. This graph goes on forever in both directions, so we can plug in any real number for x. There are no restrictions to worry about.

As an inequality, we write
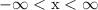`-\infty < \text{x} < \infty` to basically say "x is between negative infinity and infinity". In other words, x is anything on the real number line.

That inequality condenses into the interval notation of
`(-\infty , \infty)`

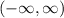
Always use curved parenthesis for either infinity, because we can't ever reach infinity. It's not a number on the number line but rather a concept.

----------------------

Now onto the range.

Recall the range is the set of possible y outputs. We look at the lowest and highest points (aka min and max) to determine the boundaries for the range.

In this case, the smallest y can get is y = -3

The largest it can get is y = 3

The range is any value of y such that
`-3 \le \text{y} \le 3` which in word form is "any value between -3 and 3, inclusive of both endpoints".

That inequality condenses to the interval notation [-3, 3]

We use square brackets to include the endpoints as part of the range.

Answer 2

`\textsf{Domain}: \quad (-\infty, \infty) \quad -\infty < x < \infty`

`\textsf{Range}: \quad [-3,3] \quad -3\leq y\leq 3`

Step-by-step explanation:

The domain of a function is the set of all possible input values (x-values).

The range of a function is the set of all possible output values (y-values).

Interval notation

• ( or ) : Use parentheses to indicate that the endpoint is excluded.
• [ or ] : Use square brackets to indicate that the endpoint is included.

Inequality notation

• < means "less than".
• > means "more than".
• ≤ means "less than or equal to".
• ≥ means "more than or equal to".

From inspection of the given graph, the function is continuous and so the domain is not restricted.

Therefore, the domain of the function is:

• Interval notation: (-∞, ∞)
• Inequality notation: -∞ < x < ∞

From inspection of the given graph, the minimum value of y is -3 and the maximum value of y is 3. Both values are included in the range.

Therefore, the range of the function is:

• Interval notation: [-3, 3]
• Inequality notation: -3 ≤ y ≤ 3