Question

A varsity cross-country team runs on a course that makes a right turn after 3 miles, and continues on one mile less than the junior varsity team's course. The junior varsity team's course runs on a straight line from the same starting point and the finish line. How long is the junior varsity team's course?

Hint: Use the Pythagorean Theorem.

7 miles
5 miles
3 miles

Answer 1

3:4:5 triangle, The junior varsity team's course is 5 miles

Answer 2

5 miles

Explanation:

We are given that A varsity cross-country team runs on a course that makes a right turn after 3 miles, and continues on one mile less than the junior varsity team's course.

The junior varsity team's course runs on a straight line from the same starting point and the finish line.

Refer the attached figure

Let the junior runs course x miles i.e. AC = x

Senior runs 3 miles i.e. BC = 3 miles

Senior continues on one mile less than the junior ie. AB = x-1

Since ΔABC is a right angles triangle

So,
`Hypotenuse^2=Perpendicular^2+Base^2`

`AC^2=AB^2+BC^2`

`x^2=(x-1)^2+3^2`

`x^2=x^2+1-2x+3^2`

`0=-2x+10`

`2x=10`

`x=(10)/(2)`

`x=5`

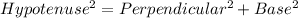
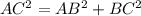
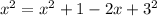
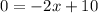
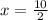
Thus the junior varsity team's course is 5 miles long.