Question

A triangular plate abc should have side ab 4 cm , side bc 6 cm and the internal angle between sides ab and bc equal to 60 degrees. What is the approximate measurement in cm that will result for the side ac?.​

Answer 1

• We know that sides AB and BC measure 6 and 4 cm and that their angles are similar, now with all this we are asked to calculate the measure of AC, for this we have two options, one to use the sine law or the other to use the cosine law.

`\qquad`
`\purple{\twoheadrightarrow\pmb{AC= \sqrt{AB^(2) + BC^(2) -2AB* BC\cos(\alpha)}}}`

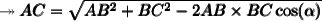
Substituting the data, we get the following:

`\qquad`
`\twoheadrightarrow\sf {AC= \sqrt{(4)^(2) + (6)^(2) -2(4)(6)\cos(60^(\circ))}}`

`\qquad`
`\twoheadrightarrow\sf {AC= √(16+ 36 -48(1/2))}`

`\qquad`
`\twoheadrightarrow\sf {AC= √(52-24)}`

`\qquad`
`\twoheadrightarrow\sf {AC= √(28)}`

`\qquad`
`\twoheadrightarrow\sf {AC= 2√(7)}`

`\qquad`
`\purple{\twoheadrightarrow\pmb{AC= 5.30\ cm}}`

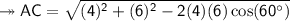
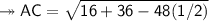
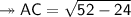
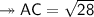
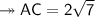
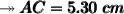
• The AC side measurement is 5.30 cm approx.