Question

The graph of f(x) = |x| is reflected across the y-axis and translated to the left 5 units. Which statement about the domain and range of each function is correct? Both the domain and range of the transformed function are the same as those of the parent function. Neither the domain nor the range of the transformed function are the same as those of the parent function. The range but not the domain of the transformed function is the same as that of the parent function. The domain but not the range of the transformed function is the same as that of the parent function.

Answer 1

its a

Explanation:

trust me

Answer 2

Both the domain and range of the transformed function are the same as those of the parent function.

Explanation:

We have,

The function
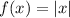`f(x)=|x|` is reflected across y-axis, which gives
`|-x|=|x|`

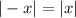
And then the function is translated to the left by 5 units.

So, the transformed function is
`g(x)=|x+5|`

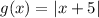
Thus, from the graph below, we get,

Domain of both functions is the set of all real numbers.

Range of both functions is the set
`\y`.

That is,

Both the domain and range of the transformed function are the same as those of the parent function.