Answer:
Option 4
(0, 1), (1, 3), (2, 9), (3, 27) set of ordered pairs could be generated by an exponential function
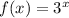 .
.
Explanation:
Given : Set of ordered pairs could be generated by an exponential function
(0, 0), (1, 1), (2, 8), (3, 27)
(0, 1), (1, 2), (2, 5), (3, 10)
(0, 0), (1, 3), (2, 6), (3, 9)
(0, 1), (1, 3), (2, 9), (3, 27)
To find : Which set?
Solution :
The general form of an exponential function is
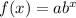
where,
a is the initial amount

b is the rate of change
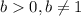
The graph of each exponential function passes through the point (0,a),
As

and

Therefore, Option 1 and 3 are false.
Now, in Option 2 and 4 first point is (0,1)
i.e,
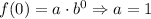
Then, The exponential function form is
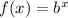
In Option 2,
Point (1,2)
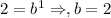
Point (2,5)
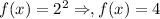
which is not correct.
Option 2 is false.
Now, In Option 4
Point (1,3)
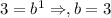
Point (2,9)
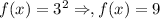 satisfying
satisfying
Point (3,27)
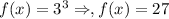 satisfying
satisfying
Option 4 is true.
Therefore, The exponential form is
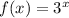
Hence, option 4 is correct.
(0, 1), (1, 3), (2, 9), (3, 27) set of ordered pairs could be generated by an exponential function
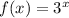 .
.