Question

Find sin θ if cot θ = - 2 and cos θ < 0

Answer 1

Given was cotθ=−21 and cot is the reciprocal of tan
therefore
tanθ=1−2
solve for the hypotenuse c since t he opposite side a=1 and the adjacent sides b=−2 were already given. that is,
c2=a2+b2
c=√(1)2+(−2)2
c=√5

Solving for sinθ

sinθ=oppositesideshypoteνse=ab

sinθ=1√5 need to rationalize
sinθ=(1√5)×√5√5

sinθ=√55

Note that the adjacent side of the angle is −2 so the angle
θ is found in the 2nd quadrant.

Answer 2

Answer: The correct answer is \frac{1}{\sqrt{5}}[/tex]

Explanation:

We are given:

`\cot \theta=(-2)/(1)`

and
`\cos \theta<0`

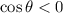
As, we know that 'cot' function is negative in second and fourth quadrants and 'cos' function is also less than 0. This function is negative in second and third quadrant.

From above, it is clear that the 'sin' function is present in second quadrant and it is positive in that quadrant.

`\cot \theta=(B)/(P)`

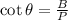
From above, it is clear that Base is 2 units and Perpendicular is 1 unit.

By Pythagoras theorem, we can easily find hypotenuse which is coming out to be
`√(5)` units.

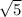`AC^2+AB^2=BC^2\\\\(1)^2+(2)^2=BC^2\\\\BC=√(5)units`

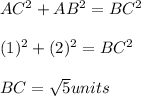
And,

`\sin \theta=(P)/(H)\\\\\sin \theta=(1)/(√(5))`

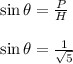
Hence, the correct answer is \frac{1}{\sqrt{5}}[/tex]