Question

What is the slope and y-intercept of line q graphed below?

3 and (-3,0)
3 and (0,1)
1/3 and (0,1)
1.3 and (-3,0)

Answer 1

The third option is the right one

Answer 2

1/3 and (0,1)

Explanation:

In a cartesian plane, we can represent a line using a general equation defined in that plane. Given a line with slope
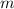`m` and a point which it passes through
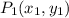`P_1(x_1,y_1)` it is possible to obtain the equation of the line from the of the slope-intercept form:

`y-y_1=m(x-x_1)`

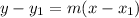
Where:

`m=(y_2-y_1)/(x_2-x_1)`

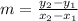
From the graph provided by the problem we can extract the two points we need.

Let:

`P_1=(x_1,y_2)=(0,1)\\P_2=(x_2,y_2)=(-3,0)`

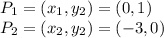
Thus:

`m=(0-1)/(-3-0) =(-1)/(-3) =(1)/(3)`

`y-1=(1)/(3) (x-0)\\\\y-1=(1)/(3) x\\\\y(x)=(1)/(3) +1`

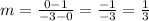
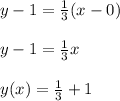
Now that we know the slope and the equation of the graph, we can easily find the y-intercept of the line. Actually you can conclude what is the y-intercept just by looking the graph, as you can see, the line crosses the y-axis at the point (0,1). However, let's find it using the equation that we found. As you may know, the line will cross the y-axis when x=0, so let's evaluate the function for x=0:

`y(0)=(1)/(3)(0) +1=0+1=1`

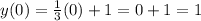
Therefore, the y-intercept of the line is (0,1).