Question

"A student made the following chart to prove that AB2 + BC2 = AC2.

Statement Justification
1. Triangle ABC is similar to triangle BDC 1. Angle ABC = Angle BDC and Angle BCA = Angle BCD
2. BC2 = AC × DC 2. BC ÷ DC = AC ÷ BC because triangle ABC is similar to triangle BDC
3. Triangle ABC is similar to triangle ABD 3. Angle ABC = Angle BAD and Angle BAC = Angle ABD
4. AB2 = AC × AD 4. AB ÷ AD = AC ÷ AB because triangle ABC is similar to triangle ABD
5. AB2 + BC2 = AC × AD + AC × DC
= AC (AD + DC)
6. Adding Statement 1 and Statement 2
7. AB2 + BC2 = AC2
Which of the first four steps is the error?"

Answer 1

Step two is incorrect

Answer 2

Given : In triangle ABC right angled at B.

To Prove :
`AB^2 + BC^2= AC^2`

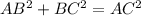
Construction: Draw B D perpendicular AC.

Proof: 1. Triangle ABC is similar to triangle BDC 1. Angle ABC = Angle BDC and Angle BCA = Angle BCD

2.
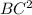`BC^2` = AC × DC 2. BC ÷ DC = AC ÷ BC because triangle ABC is similar to triangle BDC

3. Triangle ABC is similar to triangle ABD 3. Angle ABC = Angle BAD and Angle BAC = Angle ABD

4.
`AB^2` = AC × AD 4. AB ÷ AD = AC ÷ AB because triangle ABC is similar to triangle ABD

5.
`AB^2 + BC^2 = AC * AD + AC * DC`

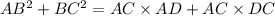
= AC (AD + DC)

6. Adding Statement 1 and Statement 2

7.
`AB^2 + BC^2= AC^2`

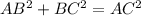
→→→Statement 3 is incorrect.It should be replaced by, Angle ABC = Angle ADB and Angle B AC = Angle BAD .