Answer:
Option C is correct
4(x+40)
Explanation:
Perimeter(P) of rectangle is given by:
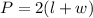
where, l is the length and w is the width of the rectangle.
As per the statement:
A playground is 50-feet long by 30-feet wide.
The length and width of the playground will each be increased by the same number of feet.
The following expression represents the perimeter of the larger playground is:
(x + 50) + (x + 30) + (x + 50) + (x + 30)
first Remove parenthesis:
x + 50+ x + 30 + x + 50+ x + 30
Combine like terms;
4x+160
using distributive property
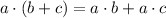 we have
we have
⇒4(x+40)
Therefore, the expression is equivalent to the expression for the perimeter of the larger playground is, 4(x+40)