Question

Consider points A(2,3) and B(6,9). Find point C on the x-axis so AC + BC is a minimum. The point that minimizes AC + BC is C ( , ).

Answer 1

the point C(x,0) = C(3,0) is the point where AC + BC is minimum.

Explanation:

Solution:

This question is very simple to solve.

We need to find the x and y elements of point C, which is on the x-axis such that AC + BC = minimum.

So,

As, we have said that, point C is on the x-axis then, it means its y co ordinate will be equals to zero.

Now, we just need to find x co ordinate of the point C.

C (x, 0) as it is on the y -axis.

So, for that, we need to take the mirror image of point B. It means, its x co-ordinate will remain same but y co-ordinate will be negative.

So, our mirror image of B(6,9) = B'(6,-9)

Now, we have to join the points A and B'. Point C, which we are trying to find is the point where this line AB' intersects with x - axis.

So,

Slope of the line AB'

m =
`(y1-y2)/(x1-x2)`

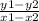
m =
`(3- - 9)/(2 - 6)` =
`(3+9)/(2-6)`

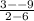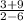
m =
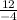`(12)/(-4)` = -3

m = slope = -3

We also know that the equation of line:

y = mx + b

where b = y-intercept.

Now, we need to find the y - intercept of this line.

y = (-3) x + b

where y = -9 and x = 6

so,

-9 = (-3) (6) + b

b = -9 + 18

b = 9 = y - intercept.

SO,

y = mx + b

and For point C(x, 0) y = 0

0 = -3x + 9

Solve for x:

3x = 9

x = 3

Hence, the point C(x,0) = C(3,0) is the point where AC + BC is minimum.