Answer:
The quadratic function,
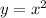 , has an x-intercept at the origin
, has an x-intercept at the origin
From
 to
to
 , the average rate of change for both functions is negative
, the average rate of change for both functions is negative
For the quadratic function,
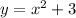 , the coordinate
, the coordinate
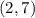 is a solution to the equation of the function
is a solution to the equation of the function
Explanation:
we have the quadratic functions
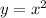
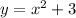
Verify each statement
case A) The quadratic function,
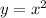 , has an x-intercept at the origin
, has an x-intercept at the origin
Remember that
The x-intercept is the value of x when the value of y is equal to zero
The point
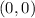 represent and x-intercept and a y-intercept
represent and x-intercept and a y-intercept
therefore
The statement is True
case B) The quadratic function,
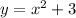 , has an x-intercept at the origin
, has an x-intercept at the origin
The quadratic function,
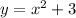 has no x-intercept
has no x-intercept
so
The statement is False
case C) From
 to
to
 , the average rate of change for both functions is positive
, the average rate of change for both functions is positive
Observing the graph from
 to
to
 , the average rate of change for both functions is negative
, the average rate of change for both functions is negative
so
The statement is False
case D) From
 to
to
 , the average rate of change for both functions is negative
, the average rate of change for both functions is negative
The statement is True
case E) For the quadratic function,
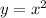 , the coordinate
, the coordinate
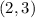 is a solution to the equation of the function
is a solution to the equation of the function
we know that
If a ordered pair is a solution of the quadratic function
then
the ordered pair must be satisfy the quadratic equation
Substitute the value of x and the value of y in the quadratic function and then compare
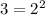
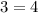 ------> is not true
------> is not true
The ordered pair is not a solution
so
The statement is False
case F) For the quadratic function,
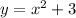 , the coordinate
, the coordinate
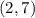 is a solution to the equation of the function
is a solution to the equation of the function
we know that
If a ordered pair is a solution of the quadratic function
then
the ordered pair must be satisfy the quadratic equation
Substitute the value of x and the value of y in the quadratic function and then compare

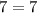 ------> is true
------> is true
The ordered pair is a solution
so
The statement is True