Question

In Fig. 15-40, block 2 of mass 2.0 kg oscillates on the end of a spring in SHM with a period of 20 ms. The position of the block is given by x = (1.0 cm) cos (ωt + π/2). Block I of mass 4.0 kg slides toward block 2 with a velocity of magnitude 6.0 m/s, directed along the spring"s length. The two blocks undergo a completely inelastic collision at time t = 5.0 ms. (The duration of the collision is much less than the period of motion.) What is the amplitude of the SHM after the collision?

Fig. 15-40

Answer 1

Amplitude= -0.03087m

Step-by-step explanation

Note that the total momentum before collision is equal to the momentum after collision.also

Energy Before Collision = Energy After Collision

the parameters are as follows

m1=6kg

m2=2kg

T=20ms=.02s

v1=6m/s

t=5ms=.005

x = (1.0 cm) cos (ωt + π/2)

There are some other equation tat could be useful

ω=2πf

ω=
`√(k/m^2)`

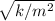
f=1/T

kinetic energy is Ek=0.5mv^2

Energy in spring=Es=0.5kx^2

Lets compute energy before collision

kinetic energy of block 1 =0.5m1v1^2

energy of block 2 which is a spring is =0.5kx^2

to find k, recall that ω=
`√(k/m^2)`

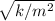
We can find ω=2πf ,

f=1/T ,f=1/0.02=50HZ

2*PI*50

ω=100πrad/s

ω=
`√(k/m^2)`

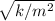
ω^2m2=k ........find the square root of both sides

k=197317

to find x, remember the position of the spring

x = (1.0 cm) cos (ωt + π/2)

ω=100πrad, t=0.005s

x = (0.01) cos (100πrad*0.005s + π/2)=

-0.01m

energy of block 1=0.5*4*6=72J

ENERGY OF SPRING=0.5*2*(100π)^2 -0.01^2=9.86J

energy before collision will be=e1+e2= 72+9.86

81.86J

energy after collision will be Eafter=0.5kx^2

0.5kx^2=0.5m*ω^2 *x^2

m=m1+m2= 6kg

ω=
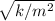`√(k/m^2)`=(197317/6)^0.5

181.3rad/s

Energy Before Collision = Energy After Collision

81.86J=(0.5)*(6)*181.3rad/s^2(x^2)

x=0.0288m

Amplitude can now be found since we have gotten all the parameters

x=A cos (ωt + π/2)

0.0288m=A cos (181.3rad/s*(0.005)+ π/2)

A= -0.03087m