Question

A curve is such that
`(dy)/(dx)` = 2(kx-1)^5 where k is a constant.

Given that the curve passes through points ( 0 , 1) , ( 1 , 8 ) find the equation of the curve.

Answer 1

Answer:
`\displaystyle y = (1)/(9)(3x-1)^(6)+(8)/(9)\\\\`

=========================================================

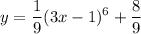
Step-by-step explanation:

Multiply dx on each side to move it over.

Doing so gets us to

`dy = 2(kx-1)^5dx`

Next, integrate both sides with respect to the dy and dx terms

`dy = 2(kx-1)^5dx\\\\ \displaystyle \int dy = \int 2(kx-1)^5dx\\\\ \displaystyle y = 2\int (kx-1)^5dx\\\\`

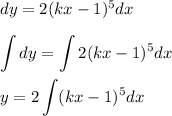
We can do a u-substitution here.

Let u = kx-1 which leads to du/dx = k which turns into
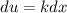`du = kdx` and rearranges to
`dx = (du)/(k)`

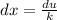
So the steps continuing forward could look like

`\displaystyle y = 2\int (kx-1)^5dx\\\\ \displaystyle y = 2\int u^5*(du)/(k)\\\\ \displaystyle y = (2)/(k)\int u^5du\\\\ \displaystyle y = (2)/(k)\left((1)/(5+1)u^(5+1)+C\right)\\\\ \displaystyle y = (2)/(k)\left((1)/(6)u^(6)+C\right)\\\\ \displaystyle y = (2)/(k)\left((1)/(6)(kx-1)^(6)+C\right)\\\\`

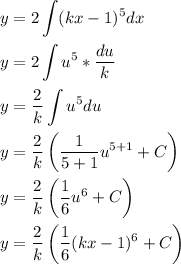
Let's plug in (x,y) = (0,1) and do a bit of algebra and solve for C. We'll get some equation in terms of k on the right hand side

`\displaystyle y = (2)/(k)\left((1)/(6)(kx-1)^(6)+C\right)\\\\ \displaystyle 1 = (2)/(k)\left((1)/(6)(k*0-1)^(6)+C\right)\\\\ \displaystyle 1 = (2)/(k)\left((1)/(6)+C\right)\\\\ \displaystyle k = 2\left((1)/(6)+C\right)\\\\ k = (1)/(3)+2C`

`3k = 1+6C\\\\ 6C = 3k-1\\\\ C = (3k-1)/(6)\\\\`

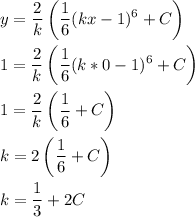
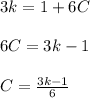
Now let's plug in (x,y) = (1,8) along with that C value. Then solve for k to get an actual number.

`\displaystyle y = (2)/(k)\left((1)/(6)(kx-1)^(6)+C\right)\\\\ 8 = (2)/(k)\left((1)/(6)(k*1-1)^(6)+(3k-1)/(6)\right)\\\\`

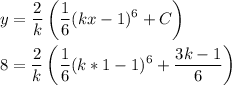
I'm skipping a bunch of steps, but you should get to
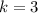`k = 3` when solving that equation. You can use a graphing calculator to find the root of that function (think of k as the input x) and the x intercept is 3.

This leads to,

`C = (3k-1)/(6)\\\\ C = (3*3-1)/(6)\\\\ C = (8)/(6)\\\\ C = (4)/(3)\\\\`

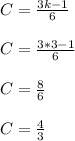
Therefore,

`\displaystyle y = (2)/(k)\left((1)/(6)(kx-1)^(6)+C\right)\\\\ y = (2)/(3)\left((1)/(6)(3x-1)^(6)+(4)/(3)\right)\\\\ \boldsymbol{y = (1)/(9)(3x-1)^(6)+(8)/(9)} \ \textbf{ which is the final answer}\\\\`

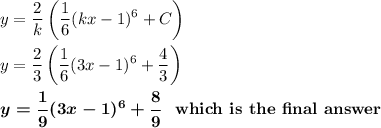
If k = 3, then,

`\displaystyle (dy)/(dx) = 2(kx-1)^5\\\\ \displaystyle (dy)/(dx) = 2(3x-1)^5\\\\`

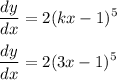
If you were to differentiate the answer function with respect to x, then you should get the dy/dx expression mentioned.