Question

An observer is standing in a lighthouse 96 feet above the level of the water. The angle of depression of a buoy is 22. What is the horizontal distance between the observer and the buoy (to the nearest whole number)?

Answer 1

238 feet.

Explanation:

Refer the attached figure .

An observer is standing in a lighthouse 96 feet above the level of the water.i.e AC = 96 feet

The angle of depression of a buoy is 22° i.e. ∠ABC = 22°

Now we are required to find the horizontal distance between the observer and the buoy i.e. BC

Now, use trigonometric ratio.

`tan\theta = (Perpendicular)/(Base)`

`tan22^(circ) = (96)/(BC)`

`0.404= (96)/(BC)`

`BC= (96)/(0.404)`

`BC= 237.62`

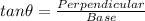
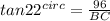
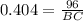
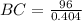
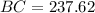
Thus the horizontal distance between the observer and the buoy is 237.62≈238 feet.