Question

One day, a person went to a horse racing area. Instead of counting the number of humans an horses, he conuted 74 heads and 196 legs. How many humans and horses were there

Answer 1

Data:

Humans (x) = 2 Legs
Horses (y) = 4 Legs

74 Heads
196 Legs

Solving:

Addition method


`\left \{ {{x + y =74} \atop {2x + 4y =196}} \right.`

Simplify by (-4) The first equation


`\left \{ {{x + y =74(-4)} \atop {2x + 4y =196}} \right.`

`\left \{ {{-4x - \diagup\!\!\!\!\!4y =-296} \atop {2x + \diagup\!\!\!\!\!4y =196}} \right.`

`\left \{ {{-4x =-296} \atop {2y =196}} \right.`

`-2x = -100.simplify(-1)`

`2x = 100`

`x = (100)/(2)`

`\boxed{x = 50}`

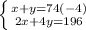
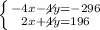
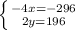
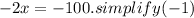
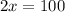
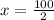
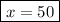
Now, to find the number of horses, I will use the following equation and I will replace the found value, we will have:


`x + y = 74`

`50+y = 74`

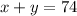
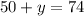
Number with incognito are to the left of the equality and numbers without incognito are to the right, remembering that when changing of side changes the signal.


`y = 74-50`

`\boxed{y = 24}`

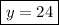
Answer:
Humans = 50
Horses = 24