Question

Given point A (-9, -9) and B (5, -2) find the coordinates of point P on the directed line segment AB in the ratio 3:4.

Answer 1

We have point P(-3,-6).

Explanation:

We want to find a point P(x,y).

Since it is on the directed line segment AB in the ratio 3:4, it means that:

`P - A = (3)/(3+4)(B - A)`

So

`P - A = (3)/(7)(B-A)`

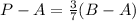
We apply this to both the x-coordinate and y-coordinate of P.

x-coordinate:

x-coordinate of A: -9

x-coordinate of B: 5

x-coordinate of P: x

So

`P - A = (3)/(7)(B-A)`

`x - (-9) = (3)/(7)(5-(-9))`

`x + 9 = (3)/(7) * 14`

`x + 9 = 6`

`x = -3`

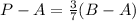
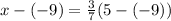
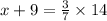
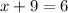
y-coordinate:

y-coordinate of A: -9

y-coordinate of B: -2

y-coordinate of P: y

So

`P - A = (3)/(7)(B-A)`

`y - (-9) = (3)/(7)(-2-(-9))`

`y + 9 = (3)/(7) * 7`

`y + 9 = 3`

`y = -6`

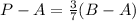
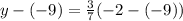
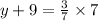
We have point P(-3,-6).