Answer:
0.28
Explanation:
Angles in standard position are angles with the initial side on the positive x-axis.
Since (7,24) lies on the terminal side of an angle, hence the line passing through the origin and point (7, 24) forms an angle with the x axis.
The slope of the line passing through the origin (0, 0) and the point (7, 24) is given by:
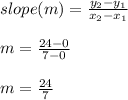
The angle θ between a straight line and the x axis is:
tanθ = m
where m is the slope of the line.
Let θ be the angle between the line with a slope of 24/7 and the x axis, therefore:
tanθ = 24 / 7
θ = tan⁻¹(24/7)
θ = 73.74°
cosθ = cos(73.74°) = 0.28