Answer:
k = 5.
Explanation:
Equation of a line:
The equation of a line has the following format:

In which m is the slope, and b is the y-intercept(y when x = 0).
Perpendicular lines
When two lines are perpendicular, the multiplication of their slopes is -1.
Perpendicular to the line y=x−285.
This line has slope 1, so the line we want to find the equation has slope
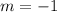
Then
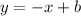
Passes through (7, 0)
This means that when
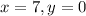 . So
. So
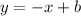


So
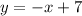
Find the value of k given that the line through (k, 2)
This means that when
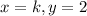 . So
. So
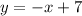
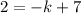

The value of k is k = 5.