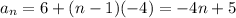An arithmetic sequence takes the form
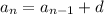
where
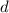
is the common difference between terms. You can solve for
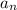
in terms of any of the previous terms of the sequence:
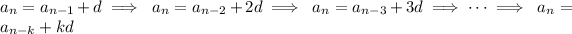
for some integer

Continuing in this way, you know that the sequence can be defined explicitly in terms of the first term
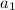
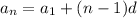
Given that the 4th term is
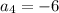
and the 11th term is

, you have the following system of equations.

Solving this system for the two unknowns yields
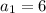
and
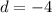
.
So, the sequence is given explicitly by