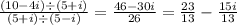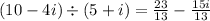 , which can be further simplified if needed.
, which can be further simplified if needed.
To evaluate the expression
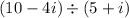 , we'll multiply both the numerator and denominator by the conjugate of the denominator to rationalize the denominator.
, we'll multiply both the numerator and denominator by the conjugate of the denominator to rationalize the denominator.
The conjugate of
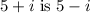 .
.
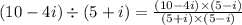
Let's perform the multiplication:
Numerator:
![\[ (10 - 4i) * (5 - i) = 50 - 10i - 20i + 4i^2 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/5w9gtnq1sc05q5qbii5i.png)
![\[ = 50 - 30i - 4 \] (Remember that \(i^2 = -1\))](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/mv6szwndq95grboivpx2.png)
![\[ = 46 - 30i \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/y5sjeaging8z8uv6f7hl.png)
Denominator:
![\[ (5 + i) * (5 - i) = 25 - 5i + 5i - i^2 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/qa0qxnm1cha7obxs73yf.png)
![\[ = 25 - i^2 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/m77ppumm51pbvdnplajz.png)
![\[ = 25 + 1 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/n3l4n9q10652uamayk4y.png)
![\[ = 26 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/zn84ekt62nl0d752epiq.png)
Now, simplify the expression: