Question

I have 17 liters of air to a balloon the is 200 kelvin. If I take the balloon to a place where the temperature is 157 kelvin, what is the new volume of the balloon be

Answer 1

The new volume of the ballon will be 13.345 L

Step-by-step explanation:

Charles's Law consists of the relationship that exists between the volume and the temperature of a certain quantity of ideal gas, which is maintained at a constant pressure, by means of a constant of proportionality that is applied directly. For a given sum of gas at a constant pressure, as the temperature increases, the volume of the gas increases and as the temperature decreases, the volume of the gas decreases.

Charles's law is a law that says that when the amount of gas and pressure are kept constant, the quotient that exists between the volume and the temperature will always have the same value:

`(V)/(T)=k`

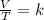
It is possible to assume that you have a certain volume of gas V1 that is at a temperature T1 at the beginning of the experiment. If you vary the volume of gas to a new value V2, then the temperature will change to T2, and it will be true:

`(V1)/(T1)=(V2)/(T2)`

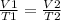
In this case:

• V1= 17 L
• T1= 200 K
• V2= ?
• T2= 157 K

Replacing:

`(17 L)/(200 K) =(V2)/(157 K)`

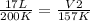
Solving:

`V2= 157 K*(17 L)/(200 K)`

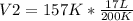
V2= 13.345 L

The new volume of the ballon will be 13.345 L