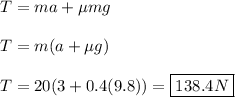Question

How much horizontal force is needed to pull a block(m=20kg) so that the block will have an

acceleration of 3m/s on a rough surface? The coefficient of kinetic friction uk is 0.4.

Answer 1

Hi there!

Recall Newton's Second Law:

`\Sigma F = ma`

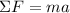
∑F = Net force (N)
m = mass (kg)

a = acceleration (m/s²)

The block will be experiencing two forces; a tension force in the direction of its acceleration (+) and a friction force (-).

`\Sigma F = T - F_K`

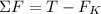
The equation for kinetic friction force is:

`F_K = \mu mg`

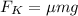
Using Newton's Second Law:

`ma = T - \mu mg`

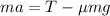
Plug in the givens and solve for 'T':

`T = ma + \mu mg\\ \\ T = m(a + \mu g)\\ \\ T = 20(3 + 0.4(9.8)) = \boxed{138.4 N}`