Given:
f(x) is an exponential function.
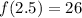
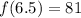
To find:
The value of f(12), to the nearest hundredth.
Solution:
The general exponential function is

For, x=2.5,
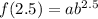
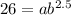 ...(i)
...(i)
For, x=6.5,
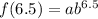
 ...(ii)
...(ii)
Divide (ii) by (i).

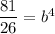
Taking 4th root on both sides, we get
![\sqrt[4]{(81)/(26)}=b](https://img.qammunity.org/2022/formulas/mathematics/college/cpg68agi59e15j1r3curqzk4amykly34nr.png)
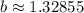
Putting b=1.32855 in (i), we get
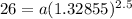
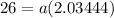
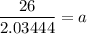
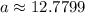
Now, the required function is
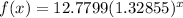
Putting x=12, we get
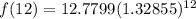
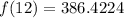
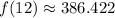
Therefore, the value of f(12) is 386.422.