Question

Ted can mow the lawn in 5 minutes by using his power mower. Galen takes 15 minutes to mow the same lawn using a push-type mower. How many minutes would the job take if the two boys worked together?

If t is the time working together, which of the following expressions represents the portion of the job that Ted will complete when the guys work together?

Answer 1

For the answer to the question above,
Minutes needed to complete full job:
Ted = 5 minutes
Galen = 15 minutes
Together = x

Amount of job completed per minute:
Ted = 1/5 of lawn
Galen = 1/15 of lawn
Together = 1/x of lawn

Equation:
1/5 + 1/15 = 1/x
3/15 + 1/15 = 1/x
4/15 = 1/x
(4/15)x = 1
x = 15/4
So the answer is 3 3/4 minutes (15/4)

Answer 2

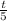`(t)/(5)` represents the portion of the job that Ted will complete when the guys work together.

Explanation:

Let t be the time working together.

Given is : Ted can mow the lawn in 5 minutes by using his power mower. Galen takes 15 minutes to mow the same lawn using a push-type mower.

Working together, they are going to complete 1 job.

So, we can show this as:

`(t)/(5) +(t)/(15) =1`

=>
`(3t+t)/(15)=1`

=>
`(4t)/(15)=1`

=>
`4t=15`

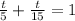
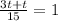
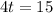
t = 3.75 minutes

So, while working together, they will take 3.75 minutes.

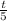`(t)/(5)` represents the portion of the job that Ted will complete when the guys work together.