Question

The exponential decay graph shows the expected depreciation for a new boat, selling for $3500, over 10 years a. Write an exponential function for the graph.

b. Use the function in part a to find the value of the boat after 9.5 years.

Answer 1

y = 3500 e^(-k⋅ 9.5)

Explanation:

The exponential decay graph shows the expected depreciation for a new boat, selling for $3500, over 10 years a. Write an exponential function for the graph.

b. Use the function in part a to find the value of the boat after 9.5 years.

Explanation:

Exponential equation is given by

y = 3500 ⋅ e^( k 9.5)

whereby:

y : value

A : constant;

k : rate of change

t : time value

In this when t =0

3500= A ⋅ e^ k 0

3500 = A

after 10 years we have

`y=3500e^(-k10)`

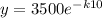
, after 9.5 years, the value of the boat is:

y = 3500 e^(-k⋅ 9.5)

k is the rate of change and it shows that it is negative because there is a depreciation in value. Note that the rate of change is not given in this case.

Answer 2

For the answer to the question above,
V(n) = a * b^n, where V(n) shows the value of boat after n years.
V(0) = 3500
V(2) = 2000

n = 0
V(0) = a * b^0 = 3500
a = 3500

V(2) = a * b^2
2000 = 3500 * b^2
b = sqrt (2000/3500)
b ≈ 0.76

V(n) = 3500 * 0.76^n

We can check it for n = 1 which is close to 2500 in the graph:
V(1) = 3500 * (0.76)^1
V(1) = 2660

And in the graph we have V(3) ≈ 1500,
V(n) = 3500 * (0.76)^3 ≈ 1536

Now n = 9.5
V(9.5) = 3500 * (0.76)^(9.5)
V(9.5) ≈ 258