Question

Find the values of a, b, and c.

a = 41, b = 144, 36
a = 77, b = 118, c = 62
a = 36, b = 103, c = 77
a = 36, b = 118, c = 62

Answer 1

a = 36, b = 118, c = 62

----------------------------

Answer 2

The correct option is 4.

Explanation:

If a transversal line intersect two parallel line, then the alternate interior angles are equal.

`a^(\circ)=36^(\circ)`

The value of a is 36.

The sum of two interior angle is equal to the exterior angle of third vertex.

`77+c=139`

`c=139-77`

`c=62`

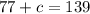
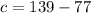
The value of c is 62.

If two angles lie on a straight line, then they are supplementary angles and their sum is 180 degree.

`b+c=180^(\circ)`

`b+62^(\circ)=180^(\circ)`

`b=180^(\circ)-62^(\circ)`

`b=118^(\circ)`

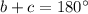
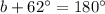
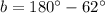
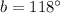
The value of b is 118.

Therefore option 4 is correct.