Question

A box that has a mass of 80 kg slides down a ramp with a 30 degree angle. The free-body diagram shows the forces acting on the box. Ignoring friction and air resistance, what is the acceleration of the box, to the nearest tenth?

-0.5 m/s2
-4.9 m/s2
-8.5 m/s2
-9.8 m/s2

Answer 1

acceleration=4.9m/s^2

Answer 2

The force responsible for sliding the block down along the ramp is the component of the weight parallel to the ramp.

The weight of the block is

`W=mg=(80 kg)(9.8 m/s^2)=784 N`

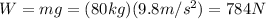
The component of the weight parallel to the ramp is

`W_(par) = W sin 30^(\circ)= (784 N)( sin 30^(\circ) )=392 N`

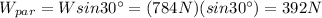
And now we can find the acceleration of the box by using Newton's second law:

`a=(F)/(m)=(392 N)/(80 kg)=4.9 m/s^2`

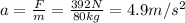
So, the correct answer is

-4.9 m/s2

(the negative just means we have taken "upward along the ramp" as positive direction)