Question

On a coordinate grid, the coordinates of vertices P and Q for Polygon PQRS are P(1, 2) and Q(−4, 2). What is the length of Side PQ of the polygon?

2 units
3 units
4 units
5 units

Answer 1

The correct option is 4.

Explanation:

Given information: P(1,2) and Q(-4,2)

We need to find the length of side PQ of the polygon.

Distance formula:

`D=√((x_2-x_1)^2+(y_2-y_1)^2)`

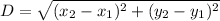
Using distance formula we get

`PQ=√((-4-1)^2+(2-2)^2)`

`PQ=√((-5)^2+(0)^2)`

`PQ=√(25)`

`PQ=5`

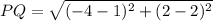
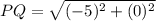
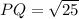
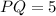
The length of side PQ of the polygon is 5 units. Therefore the correct option is 4.