Question

Victor has a credit card with an APR of 13.66%, compounded monthly. He currently owes a balance of $1,349.34. Assuming that Victor makes no purchases or payments, how much will he owe after one year, to the nearest cent?

Answer 1

A = P (1 + r/n)^nt
A = 1,349.34(1+0.1366/12)^12
A = 1545.65

answer: he will owe $1545.65 after one year

Answer 2

$1545.65.

Explanation:

We have been given that Victor has a credit card with an APR of 13.66%, compounded monthly. He currently owes a balance of $1,349.34.

To solve our given problem we will use compound interest formula.

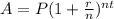`A=P(1+(r)/(n))^(nt)`, where,

A = Final amount after t years,

P = Principal amount,

r = Interest rate in decimal form,

n = Number of times interest is compounded per year,

t = Time in years.

Let us convert our given interest rate in decimal form.

`13.66\%=(13.66)/(100)=0.1366`

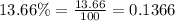
Upon substituting our given values in compound interest formula we will get,

`A=\$1,349.34(1+(0.1366)/(12))^(12*1)`

`A=\$1,349.34(1+0.011383333)^(12)`

`A=\$1,349.34(1.011383333)^(12)`

`A=\$1,349.34*1.145485275522`

`A=\$1,545.64910167397\approx \$1545.65`

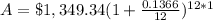
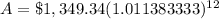
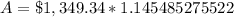
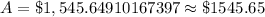
Therefore, Victor will owe an amount of $1545.65 after one year.