Question

If x² + 9y² = 26 and x × y = 4, what is the value of (x - 3y)² ??​

Answer 1

`\qquad \quad \large {\pmb{ \frak { \mid {\overline{ \underline{\purple{ \bigstar \: Required \: Answer \: \bigstar}}}}}} \mid}\\`

`\qquad` To find the value of (x - 3y) ², the binomial formula squared is: (a - b)² = a² - 2ab + b²

• If we apply binomial squared with our binomial, we get:

`\qquad`
`\purple{\twoheadrightarrow\pmb{(x-3y)^2= x^2 - \underbrace{2(x)(3y)}_(6xy) +9 y^2}}`

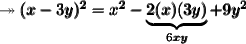
• Now, if we try to unite the corresponding terms with each one or simply call simplify, we get:

`\qquad`
`\purple{\twoheadrightarrow\sf { - 6xy+ x^2+ 9y^2}}`

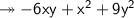
• Again, with the data included in the problem, we can get a numerical expression:

`\qquad`
`\purple{\twoheadrightarrow\sf { - 6(4)+ 26}}`

`\qquad`
`\purple{\twoheadrightarrow\sf{ -24 + 26}}`

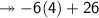
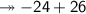
• Doing our subtraction we get that the value of the expression is equal to:

`\qquad`
`\purple{\twoheadrightarrow\pmb 2}`

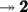
• Henceforth, The result of this expression is 2.

____________________________________