Answer:
Option (2) is correct.
The function
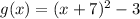 is obtained by translating
is obtained by translating
 7 units to the left and 3 units down.
7 units to the left and 3 units down.
Explanation:
Given : parent function

We have find the function g(x) such that
 is translated 7 units to the left and 3 units down to form the function g(x)
is translated 7 units to the left and 3 units down to form the function g(x)
Translation of a function is a process of shifting the parent function.
When we add or subtract anything in the brackets of parent graph, the graph will move horizontally and when we add or subtract anything outside the brackets of parent graph,the graph will move vertically.
Now when
 is translated 7 units to the left that is we are adding 7 in the brackets of parent graph
is translated 7 units to the left that is we are adding 7 in the brackets of parent graph

We get
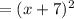
Now, the graph obtained has been translated 3 units down that is we are subtracting 3 outside the brackets of graph that is
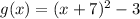
Thus, the function
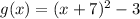 is obtained by translating
is obtained by translating
 7 units to the left and 3 units down.
7 units to the left and 3 units down.
Option (2) is correct.