Question

Given f(x) = 5x2 2 and g(x) = 2x3 (f º g)(x) is a function of degree

Answer 1

Suppose you are given the two functions f (x) = 2x + 3 and g(x) = –x2 + 5. Composition means that you can plug g(x) into f (x).

Answer 2

Degree of (fog)(x) is:

6

Explanation:

We are given
`f(x)=5x^2\ and\ g(x)=2x^3`

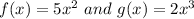
We have to find the degree of the function (fog)(x)

First of all we find (fog)(x)

(fog)(x)=f(g(x))

=
`f(2x^3)`

=
`5(2x^3)^2`

=
`5* 2^2* x^6`

=
`20x^6`

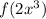
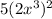
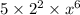
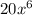
Hence, Degree of (fog)(x) is:

6

(Since degree is the highest power of x contained in the expression)